Results matching “R”

Elvis had a twin brother (who died at birth).

Historically, approximately 1/125 of all births were fraternal twins and 1/300 were identical twins. The probability that Elvis was an identical twin is approximately . . .

How does one measure the fit of a model to data? Supppose data are (y_1,...,y_n), and the estimate from the model is (x_1,...,x_n). Then one can simply measure fit by the correlation of x and y, or by the root-mean-squared error (the square root of the average of the (y_i-x_i)^2's).

When the n data points have structure, however, such simple pointwise error measures may miss the big picture. For example, suppose x and y are time series (that is, the n points are in a sequence), and x is a perfect predictor of y but just lagged by 2 time points (so that x_1=y_3, x_2=x_4, x_3=y_5, and so forth). Then we'd rather say that our error is "a lag of 2" rather than looking at the unlagged pointwise errors.

More generally, the lag need not be constant; thus, for example, there could be an error in the lag with standard deviation 1.3 time units, and an error in the prediction (after correcting for the lag) with standard deviation 0.4 units in the scale of y. Hence the title of this entry.

We have applied this idea to examples in time series and spatial statistics. Summarizing fitting error by a combination of distortion and additive error seems like a useful idea. It should be possible to do more by further decomposing fitting error.

For more, see the paper by Cavan Reilly, Phil Price, Scott Sandgathe, and myself (to appear in the journal Biometrics).

What is the value of a life, and can it be estimated by finding a wage premium for risk?

In statistics, we learn about Type 1 and Type 2 errors. For example, from an intro stat book:

A Type 1 error is commtted if we reject the null hypothesis when it is true.

A Type 2 error is committed if we accept the null hypothesis when it is false.

(Usually these are written as I and II, in the manner of World Wars and Super Bowls, but to keep things clean with later notation I'll stick with 1 and 2.)

Actually, though . . .

There has been some discussion about adjusting public opinion polls for party identification (for example, see this page by Alan Reifman, which I found in a Google search). Apparently there has been some controversy over the idea as it was applied in the 2004 Presidential election campaign. Setting aside details of recent implementations, adjusting for party ID is in general a good idea, although it's not as easy as adjusting for characteristics such as sex, age, and ethnicity, whose population proportions are well-estimated from the Census (and which change very little, if at all, during an election campaign).

Speaking of parsimony, I came across the following quotation from Commentary magazine (page 80 in the December 2004 issue):

The law of parsimony tells us that when there are alternative explanations of events, the simplest one is likely to be correct.

Commentary is a serious magazine, and this quotation (which I disagree with!) makes me wonder whether this idea of a scientific "law" is common among serious literary and political critics.

Hierarchical modeling is gradually being recognized as central to Bayesian statistics. Why? Well, one way of looking at it is that any given statistical model or estimation procedure will be applied to a series of problems--not just once--and any such set of problems corresponds to some distribution of parameter values which can themselves be modeled, conditional on any other available information. (This is the "meta-analysis" paradigm.)

Here's the spring 2005 schedule for the Family Demography and Public Policy Seminar at Columbia's School of Social Work. Lots of interesting stuff, it looks like:

Introducing A Programming Tool for Bayesian Data Analysis and Simulation using R.

Our new application for the data analysis program R eliminates most of the tedium in Bayesian simulation post-processing.

Now you can draw simulations from a posterior predictive distribution with a single line of code. You can pass random arguments to already existing functions such as mean() and sum(), and obtain simulations of distributions that you can summarize simply by typing the name of a variable on the console. It is also possible to plot credible intervals of a random vector y simply by typing plot(y)...

By enabling "random variable objects" in R, summarizing and manipulating posterior simulations will be as easy as dealing with regular numerical vectors and matrices.

Read all about it in our new paper, "Fully Bayesian Computing,".

The first beta version of the program will be soon released.

Our radon risk page (created jointly with Phil Price of the Indoor Environment Division, Lawrence Berkeley National Laboratory), is fully functional again.

You can now go over to the map, click on your state and then your county, give information about your house, give your risk tolerance (or use the default value), and get a picture of the distribution of radon levels in houses like yours. You also get an estimate of the dollar costs and lives saved from four different decision options along with a decision recommendation. (Here's an example of the output.)

We estimate that if all homeowners in the U.S. followed the instructions on this page, there would be a net savings of about $10 billion (with no additional loss of life) compared to what would happen if everybody followed the EPA's recommendation.

Aleks pointed us to an interesting article on the foundations of statistical inference by Walter Kirchherr, Ming Li, and Paul Vitanyi from 1997. It's an entertaining article in which they discuss the strategy of putting a prior distribution on all possible models, with higher prior probabilities for models that can be described more concisely. Thus linking Bayesian inference with Occam's razor.

I'm not convinced, though. They've convinced me that their model has nice mathematical properties but I don't see why it should work for problems I've worked on such as estimating radon levels or incumbency advantage or the probability of having a death sentence overturned or whatever.

Mark Hansen and Bin Yu have worked on applying this "minimum description length" idea to regression modeling, and I think it's fair to say that these ideas are potentially very useful without being automatically correct or optimal in the sense that seems to be implied by Kirchherr et al. in the paper linked to above.

We had our first annual statistical teaching, application, and research conference here at Columbia last Friday. The goal of the conference was to bring together people at Columbia who do quantitative research, or who teach statistics, but are spread out among many departments and schools (including biology, psychology, law, medical informatics, economics, political science, sociology, social work, business, and many others, as well as statistics and biostatistics).

Both the application/research and teaching sessions went well, with talks that were of general interest but went into some depth, and informed and interesting discussions.

Multiple imputation is the standard approach to accounting for uncertainty about missing or latent data in statistics. Multiple imputation can be considered as a special case of Bayesian posterior simulation, but its focus is not so much on the imputation model itself as on the imputations themselves, which can be used, along with the observed data, in subsequent "completed-data analyses" of the dataset that would have been observed (under the model) had there been no missingness.

How can we check the fit of models in the presence of missing data?

The U.S. is over-polled. You might have noticed this during the recent election campaign when national polls were performed roughly every 2 seconds. (This graph shows the incredible redundancy just from the major polling organizations.)

It would be interesting to estimate the total number of persons polled during the last year. A few years ago, I refereed a paper for Public Opinion Quarterly reporting on a survey that asked people, How many times were you surveyed in the past year? I seem to recall that the average response was close to 1.

My complaint is not new, but this recent campaign was particularly irritating because it became commonplace for people to average batches of polls to get more accurate estimators. As news consumers, we're like gluttons stuffing our faces with 5 potato chips at a time, just grabbing them out of the bag.

A lot has been written in statistics about "parsimony"--that is, the desire to explain phenomena using fewer parameters--but I've never seen any good general justification for parsimony. (I don't count "Occam's Razor," or "Ockham's Razor," or whatever, as a justification. You gotta do better than digging up a 700-year-old quote.)

Maybe it's because I work in social science, but my feeling is: if you can approximate reality with just a few parameters, fine. If you can use more parameters to fold in more information, that's even better.

In practice, I often use simple models--because they are less effort to fit and, especially, to understand. But I don't kid myself that they're better than more complicated efforts!

My favorite quote on this comes from Radford Neal's book, Bayesian Learning for Neural Networks, pp. 103-104:

Sometimes a simple model will outperform a more complex model . . . Nevertheless, I believe that deliberately limiting the complexity of the model is not fruitful when the problem is evidently complex. Instead, if a simple model is found that outperforms some particular complex model, the appropriate response is to define a different complex model that captures whatever aspect of the problem led to the simple model performing well.

Exactly!

P.S. regarding the title of this entry: there's an interesting paper by Albert Hirschman with this title.

Eduardo writes:

I'm sure most of you noticed that our blog disappeared for a while last week.

Some f&*^ing kid in Michigan of all places hacked into my
stat.columbia.edu account through the Wiki. I think the Wiki security problems are now fixed, and have also learned the hard way not to rely on anyone else to back things up!

Anyway, I just wanted to let everyone know that the blog is now functional again, and getting close to being back to its old glory. Most if not all of the entries are back up. I'll work on comments tomorrow. The uploaded files and links were lost. I'll replace the ones I have access to, but you might want to check your own entries and update links and pictures (same goes for the Wikis). All authors have the same user names as they were before, and passwords have been set back to the original ones I made up (let me know if you don't know your password).

I apologize for the interruption!

sam

Christopher Avery, Mark Glickman, Caroline Hoxby, and Andrew Metrick wrote a paper recently ranking colleges and universities based on the "revealed preferences" of the students making decisions about where to attend. They apply, to data on 3000 high-school students, statistical methods that have been developed to evaluate chess players, hospitals, and other things. If a student has been accepted to colleges A and B, and he or she chooses to attend A, this counts as a "win" for A and a "loss" for B.

Or maybe the right quote is, "It's what you learn after you know it all that counts." In any case, Chris Genovese and I have a little discussion on his blog on the topic of estimating the uncertainty in function estimates. My part of the discussion is pretty vague, but Chris is promising a link to an actual method, so this should be interesting.

Jasjeet Sekhon sent me the following note regarding analyses of votes for Bush and Kerry in counties in Florida:

Hi Sam and Andrew, I just saw your blog entries on the e-voting controversy. A week ago I posted a short research note about the optical voting machine vs. DRE issue in Florida. It is entitled "The 2004 Florida Optical Voting Machine Controversy: A Causal Analysis Using Matching". In this note, I try to obtain balance on all of the baseline variables I can find, and the results give NO support to the conjecture that optical voting machines resulted in fewer Kerry votes than the DREs would have. Of course, one really needs precinct-level data to make inferences to many of the counties in the state.

Also of interest to you may be a research note by Jonathan Wand.
He has also obtained a ZERO effect for optical
machines by using Walter's and mine robust estimator. In that
analysis, ALL of the counties are used. Wand introduces a key new
variable: he uses campaign finance contributions as a covariate. But
has he notes the linearity assumption is dubious with this dataset.

Cheers,
Jas.

Many of the wells used for drinking water in Bangladesh and other South Asian countries are contaminated with natural arsenic, affecting an estimated 100 million people. Arsenic is a cumulative poison, and exposure increases the risk of cancer and other diseases.

Is my well safe?

One of the challenges of reducing arsenic exposure is that there's no easy way to tell if your well is safe. Kits for measuring arsenic levels exist (and the evidence is that aresenic levels are stable over time in any given well), but we and other groups are just beginning to make these kits widely available locally.

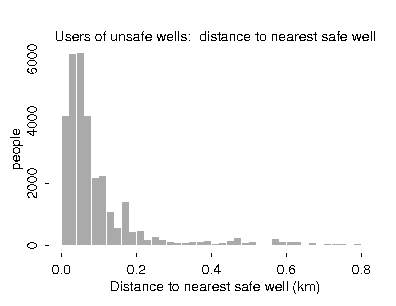
Suppose your neighbor's well is low in arsenic. Does this mean that you can relax? Not necessarily. Below is a map of arsenic levels in all the wells in a small area (see the scale of the axes) in Araihazar upazila in Bangladesh:

Blue and green dots are the safest wells, yellow and orange exceed the Bangladesh standard of 50 micrograms per liter, and red and black indicate the highest levels of arsenic.

Bad news: dangerous wells are near safe wells

As you can see, even if your neighbor has a blue or green well, you're not necessarily safe. (The wells are located where people live. The empty areas between the wells are mostly cropland.) Safe and dangerous wells are intermingled.

Good news: safe wells are near dangerous wells

There is an upside, though: if you currently use a dangerous well, you are probably close to a safe well. The following histogram shows the distribution of distances to the nearest safe well, for the people in the map above who currently (actually, as of 2 years ago) have wells that are yellow, orange, red, or black:

Switching and sharing

So if you are told where that safe well is, maybe you can ask your neighbor who owns that well to share. In fact, a study by Alex Pfaff, Lex van Geen, and others has found that people really do switch wells when they are told that their well is unsafe. We're currently working on a cell-phone-based communication system to allow people in Bangladesh to get some of this information locally.

General implications for decision analysis

This is an interesting example for decision analysis because decisions must be made locally, and the effectiveness of various decision strategies can be estimated using direct manipulation of data, bypassing formal statistical analysis.

Other details

Things are really more complicated than this because the depth of the well is an important predictor, with different depths being "safe zones" in different areas, and people are busy drilling new wells as well as using and measuring existing ones. Some more details are at our papers in Risk Analysis and Environmental Science & Technology.

Here is one of my favorite homework assignments. I give students the following twenty data points and ask them to fit y as a function of x1 and x2.

x1 x2 y
0.4 19.7 19.7
2.8 19.1 19.3
4.0 18.2 18.6
6.0 5.2 7.9
1.1 4.3 4.4
2.6 9.3 9.6
7.1 3.6 8.0
5.3 14.8 15.7
9.7 11.9 15.4
3.1 9.3 9.8
9.9 2.8 10.3
5.3 9.9 11.2
6.7 15.4 16.8
4.3 2.7 5.1
6.1 10.6 12.2
9.0 16.6 18.9
4.2 11.4 12.2
4.5 18.8 19.3
5.2 15.6 16.5
4.3 17.9 18.4

[If you want to play along, try to fit the data before going on.]

Gonzalo pointed me to a paper by Michael Hout, Laura Mangels, Jennifer Carlson, and Rachel Best at Berkeley that points out some systematic differences between election outcomes in e-voting and non-e-voting counties in Florida. To jump to the punch line: they have found an interesting pattern, which closer study suggests arises from just two of the e-voting counties: Broward and Palm Beach, which unexpectedly swung about 3% toward Bush in 2004. They also make some pretty strong causal claims which I would think should be studied further, but with some skepticism.

Pretty pictures

Before getting to a discussion of this paper, let me show you a few pictures (adapted from an analysis performed Bruce Shaw here at Columbia).

First, a scatterplot of the counties in Florida, displaying the change in the Republican vote percentage from 2000 to 2004, plotting vs. the Republican vote percentage in 2000 (in both cases, using the Republican % of the two-party vote). Red circles indicate the counties that used e-voting in 2000, and black circles used optical scans. The radius of each circle is roughly proportional to the log of the #votes in the county.

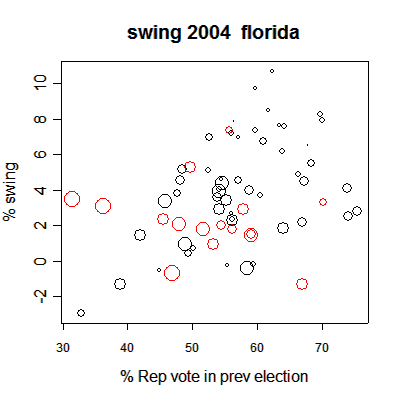
There are three obvious patterns in the figure:

1. The e-voting counties, especially the largest of them, were more Democrat-leaning.

2. For the optical scan counties, there was a consistent trend that the counties that favored Bush more in 2000, tended to move even more toward Bush in 2000.

3. For the e-voting counties, no such trend is apparent. In particular, the two large red circles on the left of the plot (Broward and Palm Beach) moved strongly toward the Republicans.

Next: looking at previous years, and commenting on the Hout et al. paper.

Juan Robalino and Alex Pfaff have written a paper on estimating the factors that influence the decision of Costa Rican farmers to clear forest land.

This is an important question because, as they note in the article,

Rural areas of developing countries contain almost the entire stock of the world's tropical forest. The poverty levels in these areas and the world demands for forest conservation have generated discussions concerning the determinants of deforestation and the appropriate policies for conservation.

When a neighbors have cleared their land of forest, a farmer is likely to clear his or her land also. However, as Robalino and Pfaff note, neighboring plots of land will have many potentially unobserved similarities, and so mere correlation between neighbors' decisions is not sufficient evidence of causation.

Rosalino and Pfaff estimate the effect of neighbors' actions on individual deforestation decisions using a two-stage probit regression. In their model, they treat the slopes of the neighboring farmers' land as an instrumental variable. I don't fully understand instrumental variables, but this looks like an interesting example as well as being an important application.

A common design in an experiment or observational study is to have two groups--treated and control units--and to take "before" and "after" measurements on each unit. (The basis of any experimental or observational study is to compare treated to control units; for example, there might be improvement from before to after whether or not a treatment was applied.)

The usual model

The usual statistical model for such data is a regression of "after" on "before" with parallel lines for treatment and control groups, with the difference between the lines representing the treatment effect. The implication is that the treatment has a constant effect, with the only difference between the two groups being an additive shift.

We went back and looked at some before-after data that we had kicking around (two observational studies from political science and an educational experiment) and found that this standard model was not true--in fact, treatment and control groups looked systematically different, in consistent ways.

Actually...

In the examples we studied, the correlation between "before" and "after" measurements was higher in the control group than in the treatment group. When you think about this, it makes sense: applying the "treatment" induces changes in the units, and so it is reasonable to expect a lower correlation with the "before" measurement.

Another way of saying this is: if the treatment effect varies (instead of being a constant), it will reduce the before-after correlation. So our finding can be interpreted as evidence that treatment effects generally vary, which of course makes sense.

In fact, the only settings we found where the controls did not have a higher before-after correlation than treated units, were when treatment effects were essentially zero.

The term "decision analysis" has multiple meanings in Bayesian statistics. When we use the term here, we are not talking about problems of parameter estimation, squared error loss, etc. Rather, we use "decision analysis" to refer to the solution of particular decision problems (such as in medicine, public health, or business) by averaging over uncertainties as estimated from a probability model. (See here for an example.)

That said, decision analysis has fundamental difficulties, most notably that it requires one to set up a utility function, which on one hand can be said to represent subjective feelings but on the other hand is presumably solid enough that it is worth using as the basis for potentially elaborate calculations.

From a foundational perspective, this problem can be resolved using the concept of institutional decision analysis.

Partisan voting is back. It is fed by new issues that fall on the
left/right ideological continuum. These are likely to be social,
religious and racial issues. This trend has led to an increase in
rationalization and, therefore, a weakening role for
retrospection. Voters are less willing to vote based on past
performance but more willing to offer evaluations that, even if
untrue, rationalize their partisan predispositions and vote
choices.

This is one of my three dissertation papers. It is the basis of my job talk. Any thoughts, citations, etc. are appreciated.

We call an Environmental Index an agglomeration of data compiled to provide a relative measure of environmental conditions. Environmental data is often sparse or non-random missing; many concepts, such as environmental risk or sustainability, are still being defined; indexers must balance modeling sophistication with modeling facility and model interpretability. We review our approaches to these constraints in the construction of the 2002 ESI and the UN Development Programme risk report.

This presentation, delivered at INFORMS2004, is a sketch of some work completed at CIESIN from 2001-2004 - where I spent two years as a gra. A paper has been submitted on diagnostics for multiple imputation used in the ESI. I hope to generate a paper on the bayesian network aggregation used in the risk index. I'm talking dec. 9th.

Lisa Levine sent me this interesting combinatorical explanation (written by Harry Graber, it seems) of why good anagrams are possible. He uses an example an anagram transcription by Richard Brodie of the Khayyam/Fitzgerald Rubaiyat (and here's another webpage with information on it).

Graber writes:

Radon is a radioactive gas that is generally believed to cause lung cancer, even in low concentrations, and might exists in high concentrations in the basement of your house (see the map).

The EPA recommends that you should test your home for radon and then fix the problem if your measurement is 4 picoCuries per liter or higher. We estimate that this strategy, if followed, would cost about $25 billion and save about 110,000 lives over the next thirty years.

We can do much better by using existing information on radon levels to target homes that are likely to have high levels. If meausrements are more targeted, we estimate that the same savings of 110,000 lives can be achieved at a cost of only $15 billion. The problem with the EPA's recommendation is that, by measuring everyone, including those who will probably have very low radon, it increases the number of false alarms--high measurements that occur just by chance in low-radon houses.

We found formal decision analysis to be a useful tool in quantifying the recommendations of where to measure and remediate. (For more details, see Section 22.4 of Bayesian Data Analysis and this paper).

Click here to see what to do for your house.

Carrie McLaren has an interesting interview with Frank Ackerman and Lisa Heinzerling in the current Stay Free magazine, on the topic of cost-benefit analysis, as it is used in environmental regulations (for example, how much money is it worth spending to reduce arsenic exposures by a specified amount). Apparently, a case of chronic bronchitis has been judged to have a cost of $260,000, and IQ points are worth $8300 each. Ackerman and Heinzerling argue that cost-benefit analysis is "fundamentally flawed," basically because it involves a lot of arbitrary choices that allow regulators to do whatever they want and justify their choices with numbers.

This made me a little worried, since I've done some cost-benefit analysis myself! In particular, I'm sympathetic to the argument that cost-benefit analysis requires arbitrary choices of the value of a life (for example). Garbage in, garbage out, and all that. But, on the plus side, cost-benefit analysis allows one to quantify the gains from setting priorities. Even if you don't "believe" a particular value specified for value of a life, you can calculate conditional on that assumed value, as a starting point to understanding the full costs of different decision options.

With this mixture of interest and skepticism as background, I was interested to read the following exchange in the Stay Free interview:

What can be done to move cross-validation from a research idea to a routine step in Bayesian data analysis?

Cross-validation is a method for evaluating model using the following steps: (1) remove part of the data, (2) fit the model the smaller dataset excluding the removed part, (3) use the fitted model to predict the removed part, (4) summarizing the prediction error by comparing to the actual left-out data. The entire procedure can then be repeated with different pieces of data left out. Various versions of cross-validation compare to different choices of leaving out data--for example, removing just one point, or removing a randomly-selected 1/10 of the data, or removing half the data.

Several conceptual and computational challenges arise when attempting to apply cross-validation for Bayesian multilevel modeling.

Background on cross-validation

Unlike predictive checking (which is a method to discover ways in which a particular model does not fit the data), cross-validation is used to estimate the predictive error of a model and to compare models (choosing the model with lower estimated predictive error).

Computational challenges

With leave-one-out cross-validation, the model must be re-fit n times. That can take a long time, since fitting a Bayesian model even once can require iterative computation!

In classical regression, there are analytic formulas for estimates and predictions with one data point removed. But for full Bayesian computation, there are no such formulas.

Importance sampling has sometimes been suggested as a solution: if the posterior distribution is p(theta|y), and we remove data point y_i, then the leave-one-out posterior distribution is p(theta|y_{-i}), which is proportional to p(theta|y)/p(y_i|theta). One could then just use draws of theta from the posterior distribution and weight by 1/p(y_i|theta). However, this isn't a great practical solution since the weights, 1/p(y_i|theta), are unbounded, so the importance-weighted estimate can be unstable.

I suspect a better approach would be to use importance resampling (that is, sampling without replacement from the posterior draws of theta using 1/p(y_i|theta) as sampling weights) to get a few draws from an approximate leave-one-out posterior distribution, and then use a few steps of Metropolis updating to get closer.

For particular models (such as hierarchical linear and generalized linear models) it would also seem reasonable to try various approximations, for example estimating predictive errors conditional on the posterior distribution of the hyperparameters. If we avoid re-estimating hyperparameters, the computation becomes much quicker--basically, it's classical regression--and this should presumably be reasonable when the number of groups is high (another example of the blessing of dimensionality!).

Leaving out larger chunks; fewer replications

The computational cost of performing each cross-validation suggests that it might be better to do fewer. For example, instead of leaving out one data point and repeating n times, we could leave out 1/10 of the data and repeat 10 times.

Multilevel models: cross-validating clusters

When data have a multilevel (hierarchical) structure, it would make sense to cross-validate by leaving out data individually or in clusters, for example, leaving out a student within a school or leaving out an entire school. The two cross-validations test different things. Thus, there would be a cross-validation at each level of the model (just as there is an R-squared at each level).

Comparing models in the presence of lots of noise, as in binary-data regression

A final difficulty of cross-validation is that, in models where the data-level variation is high, most of the predictive error will be due to this data-level variation, and so vastly different models can actually have similar levels of cross-validation error.

Shouhao and I have noticed this problem in a logistic regression of vote preferences on demographic and geographic predictors. Given the information we have, most voters are predicted to have a probability between .3 and .7 of supporting either party. The predictive root mean squared error is necessarily then close to .5, no matter what we do with the model. However, when evaluating errors at the group level (leaving out data from an entire state), the cross-validation appears to be more informative.

Summary

Cross-validation is an important technique that should be standard, but there is no standard way of applying it in a Bayesian context. A good summary of some of the difficulties is in the paper, "Bayesian model assessment and comparison using cross-validation predictive densities," by Aki Vehtari and Jouko Lampinen, Neural Computation 14 (10), 2339-2468. Yet another idea is DIC, which is a mixed analytical/computational approximation to an esitmated predictive error.

I don't really know what's the best next step toward routinizing Bayesian cross-validation.

A wise statistician once told me that to succeed in statistics, one could either be really smart, or be Bayesian. He was joking (I think), but maybe an appropriate correlary to that sentiment is that to succeed in Bayesian statistics, one should either be really smart, or be a good programmer. There's been an explosion in recent years in the number and type of algorithms Bayesian statisticians have available for fitting models (i.e., generating a sample from a posterior distribution), and it cycles: as computers get faster and more powerful, more complex model-fitting algorithms are developed, and we can then start thinking of more complicated models to fit, which may require even more advanced computational methods, which creates a demand for bigger better faster computers, and the process continues. As new computational methods are developed, there is rarely well-tested, publicly-available software for implementing the algorithms, and so statisticians spend a fair amount of time doing computer programming. Not that there's anything wrong with that, but I know I at least have been guilty (once or twice, a long time ago) of being a little bit lax about making sure my programs actually work. It runs without crashing, it gives reasonable-looking results, it must be doing the right thing, right? Not necessarily, and this is why standard debugging methods from computer science and software engineering aren't always helpful for testing statistical software. The point is that we don't know exactly what the software is supposed output (if we knew what our parameter estimates were supposed to be, for example, we wouldn't need to write the program in the first place), so if software has an error that doesn't cause crashes or really crazy results, we might not notice.

So computing can be a problem. When fitting Bayesian models, however, it can also come to the rescue. (Like alcohol to Homer Simpson, computing power is both the cause of, and solution to, our problems. This particular problem, anyway.) The basic idea is that if we generate data from the model we want to fit and then analyze those data under the same model, we'll know what the results should be (on average), and can therefore test that the software is written correctly. Consider a Bayesian model p(θ)p(y|θ), where p(y|θ) is the sampling distribution of the data and p(θ) is the prior distribution for the parameter vector θ. If you draw a "true" parameter value θ0 from p(θ), then draw data y from p(y|θ0), and then analyze the data (i.e., generate a sample from the posterior distribution, p(θ|y)) under this same model, θ0 and the posterior sample will both be drawn from the same distribution, p(θ|y), if the software works correctly. Testing that the software works then amounts to testing that θ0 looks like a draw from p(θ|y). There are various ways to do this. Our proposed method is based on the idea that if θ0 and the posterior sample are drawn from the same distribution, then the quantile of θ0 with respect to the posterior sample should follow a Uniform(0,1) distribution. Our method for testing software is as follows:

1. Generate θ0 from p(θ)
2. Generate y from p(y|θ0)
3. Generate a sample from p(θ|y) using the software to be tested.
4. Calculate the quantile of θ0 with respect to the posterior sample. (If θ is a vector, do this for each scalar component of θ.)

Steps 1-4 comprise one replication. Performing many replications gives a sample of quantiles that should be uniformly distributed if the software works. To test this, we recommend performing a z test (individually for each component of θ) on the following transformation of the quantiles: h(q) = (q-.5)2. If q is uniformly distributed, h(q) has mean 1/12 and variance 1/180. Click here for a draft of our paper on software validation [reference updated], which explains why we (we being me, Andrew Gelman, and Don Rubin) like this particular transformation of the quantiles, and also presents an omnibus test for all components of θ simultaneously. We also present examples and discuss design issues, the need for proper prior distributions, why you can't really test software for implementing most frequentist methods this way, etc.

This may take a lot of computer time, but it doesn't take much more programming time than that required to write the model-fitting program in the first place, and the payoff could be big.

Here's another journalistic account of the Red/Blue divide. It's from today's (11/03/04) NY Times by Nicholas D. Kristof. He asserts that the poor (from America's heartland) vote Republican and the wealthy (from suburban America) vote Democratic.

In the aftermath of this civil war that our nation has just fought, one result is clear: the Democratic Party's first priority should be to reconnect with the American heartland.

I'm writing this on tenterhooks on Tuesday, without knowing the election results. But whether John Kerry's supporters are now celebrating or seeking asylum abroad, they should be feeling wretched about the millions of farmers, factory workers and waitresses who ended up voting - utterly against their own interests - for Republican candidates.

One of the Republican Party's major successes over the last few decades has been to persuade many of the working poor to vote for tax breaks for billionaires. Democrats are still effective on bread-and-butter issues like health care, but they come across in much of America as arrogant and out of touch the moment the discussion shifts to values.

"On values, they are really noncompetitive in the heartland," noted Mike Johanns, a Republican who is governor of Nebraska. "This kind of elitist, Eastern approach to the party is just devastating in the Midwest and Western states. It's very difficult for senatorial, Congressional and even local candidates to survive."

In the summer, I was home - too briefly - in Yamhill, Ore., a rural, working-class area where most people would benefit from Democratic policies on taxes and health care. But many of those people disdain Democrats as elitists who empathize with spotted owls rather than loggers.

One problem is the yuppification of the Democratic Party. Thomas Frank, author of the best political book of the year, "What's the Matter With Kansas: How Conservatives Won the Heart of America," says that Democratic leaders have been so eager to win over suburban professionals that they have lost touch with blue-collar America.

"There is a very upper-middle-class flavor to liberalism, and that's just bound to rub average people the wrong way," Mr. Frank said. He notes that Republicans have used "culturally powerful but content-free issues" to connect to ordinary voters.

To put it another way, Democrats peddle issues, and Republicans sell values. Consider the four G's: God, guns, gays and grizzlies.

One-third of Americans are evangelical Christians, and many of them perceive Democrats as often contemptuous of their faith. And, frankly, they're often right. Some evangelicals take revenge by smiting Democratic candidates.

Then we have guns, which are such an emotive issue that Idaho's Democratic candidate for the Senate two years ago, Alan Blinken, felt obliged to declare that he owned 24 guns "and I use them all." He still lost.

As for gays, that's a rare wedge issue that Democrats have managed to neutralize in part, along with abortion. Most Americans disapprove of gay marriage but do support some kind of civil unions (just as they oppose "partial birth" abortions but don't want teenage girls to die from coat-hanger abortions).

Finally, grizzlies - a metaphor for the way environmentalism is often perceived in the West as high-handed. When I visited Idaho, people were still enraged over a Clinton proposal to introduce 25 grizzly bears into the wild. It wasn't worth antagonizing most of Idaho over 25 bears.

"The Republicans are smarter," mused Oregon's governor, Ted Kulongoski, a Democrat. "They've created ... these social issues to get the public to stop looking at what's happening to them economically."

"What we once thought - that people would vote in their economic self-interest - is not true, and we Democrats haven't figured out how to deal with that."

Bill Clinton intuitively understood the challenge, and John Edwards seems to as well, perhaps because of their own working-class origins. But the party as a whole is mostly in denial.

To appeal to middle America, Democratic leaders don't need to carry guns to church services and shoot grizzlies on the way. But a starting point would be to shed their inhibitions about talking about faith, and to work more with religious groups.

Otherwise, the Democratic Party's efforts to improve the lives of working-class Americans in the long run will be blocked by the very people the Democrats aim to help.

Do we still see an (income) paradox in 2004? Let's first look at the state level. A quick correlation between median family income and percent Republican vote shows a -0.41 pearson's (and -.46 spearman) correlation. Both are significant. So at the state level, it looks like lower income states are voting for the Republican candidate and higher income states are voting for the Democratic candidate.

What about the individual level? Let's look at the exit polls.

R D
<15K 36% 63%
$15-30K 41 58
$30-50K 48 51
$50-75K 55 44
$75-100K 53 46
$100-150K 56 43
$150-200K 57 43
>$200K 62 37

So it looks like the paradox is alive an kicking. So do we still believe it's an aggregation problem? Is the paradox only alive in rural areas, but dead in urban areas? More to come...

In political science, there is an increasing availability of cross country survey data, such as the Comparative Study of Electoral Systems (CSES, 33 countries) and the World Values Study (WVS, more than 70 countries). What is the best way to analyze data with this structure, specially when one suspects a great deal of heterogeneity across countries?

The structure of cross-section survey data has a small number of countries relative to the number of observations in each country. This, of course, is the exact opposite of panel data. Methods such as random effects logit or probit work well under the assumption that the number of countries goes to infinity and the number of observations in each country is small. In fact, the computational strategies (Gauss-Hermite quadrature and variants) are only guaranteed to work when the number of observations per country is small. Another useful technique, robust standard errors clustered by country, is also known to provide overconfident standard errors when the number of clusters (in our case, countries) is small. Bayesian Multilevel models would work, but are we really worried about efficiency when we have more than 1000 observations per country?

Different people in the discipline have been suggesting a two step strategy. The first step involves estimating separate models for each country, obviously including only variables which vary within countries. Then one estimates a model for each coefficient as a function of contextual level variables (that are the main interest). Since the number of observations in each country is large, under standard assumptions the individual level estimates are consistent and asymptotically normal. We can take each of the individual level estimates to be a reduced form parameter of a fully interactive model.

The country level model might be estimated via ordinary least squares, or one of the various weighting schemes proposed in the meta-analysis literature (in addition to, of course, Bayesian Meta-Analysis). What are the potential problems and advantages of such approach? Here are the ones I can think of:

Advantages :

1) We don't need to give a distribution for the individual level estimates. That is, one need not to assume that the "random effects" have, for example, a normal distribution. The coefficients are simply estimated from the data.

2) Computational Speed when compared to full MCMC methods.

3) Some monte carlo evidence showing that the standard errors are closer to the nominal levels than alternative strategies.

Disadvantages:

1) When fitting discrete choice models (e.g. probit, logit) we need to worry about the scale invariance (we estimate beta/sigma in each country, but we do not constraint sigma to be the same across countries). Any ideas on how to solve this problem?

2) Efficiency losses (which I think are minimal)

Further issues:

1) Does it have any advantages over an interactive regression model with, say, clustered standard errors? Or GEE? Relatedly, do we interpret the effects as regular conditional (i.e. random effects) model?

2) Is it worrisome to fit a maximum likelihood in the first step and a bayesian model at the second?

We (John Huber, Georgia Kernell and Eduardo Leoni) took this approach in this paper, if you want to see an application. It is still a very rough draft, comments more than welcome.

There are a bunch of methods floating around for estimating ideal points of legislators and judges. We've done some work on the logistic regression ("3-parameter Rasch") model, and it might be helpful to see some references to other approaches.

I don't have any unified theory of these models, and I don't really have any good reason to prefer any of these models to any others. Just a couple of general comments: (1) Any model that makes probabilistic predictions can be judged on its own terms by comparing to actual data. (2) When a model is multidimensional, the number of dimensions is a modeling choice. (In our paper, we use 1-dimensional models but in any given application we would consider that as just a starting point. More dimensions will explain more of the data, which is a good thing.) I do not consider the number of dimensions to be, in any real sense, a "parameter" to be estimated.

Now, on to the models.

Most of us are familiar with the Poole and Rosenthal model for ideal points in roll-call voting. The website has tons of data and some cool dynamic graphics.

For a nice overview of distance-based models, see Simon Jackman's webpage on ideal-point models. This page has a derivation of the model from first principles along with code for fitting it yourself.

Aleks Jakulin has come up with his own procedure for hierarchical classification of legislators using roll-call votes and has lots of detail and cool pictures on his website. He also discusses the connection of these measures to voting power.

Jan de Leeuw has a paper on ideal point estimation as an example of principal component analysis. The paper is mostly about computation but it has an interesting discussion of some general ideas about how to model this sort of data.

Any other good references on this stuff? Let us know.

In his paper, Homer Gets a Tax Cut: Inequality and Public Policy in the American Mind, Larry Bartels studies the mystery of why most Americans support repeal of the estate tax, even at the same time that they believe the rich should pay more in taxes.

For example, as described in Bartels's article for The American Prospect,

In the sample as a whole, almost 70 percent favored repeal [of the estate tax]. But even among people with family incomes of less than $50,000 (about half the sample), 66 percent favored repeal. . . . Among people who said that the difference in incomes between rich and poor has increased in the past 20 years and that it is a bad thing, 66 percent favored repeal. . . . Among people who said that the rich are asked to pay too little in federal income taxes (more than half the sample), 68 percent favored repeal. And, most remarkably, among those respondents sharing all of these characteristics -- the 11 percent of the sample with the strongest conceivable set of reasons to support the estate tax -- 66 percent favored repeal.
Bartels's basic explanation of this pattern is that most people are confused, and they (mistakenly) think the estate tax repeal will benefit them personally.

His explanation sounds reasonable to me, at least in explaining many peoples' preferences on the issue. But I wonder if ideology can explain some of it, too. If you hold generally conservative views of the economy and politics, then the estate tax might seem unfair--and having this norm of fairness would be consistent with other views such as "the rich should have to pay their share." The point is that voters don't necessarily think in terms of total tax burden; rather, they can legitimately view each separate tax on its own and rate it with regard to fairness, effectiveness, etc.

Statistically, I'm envisioning a mixture model of different types of voters, some of whom support tax cuts for ideological reasons (I don't mean to "ideological" negatively here--I'm just referring to those people who tend to support tax cuts on principle), others who support the estate tax repeal because they (generally falsely) think it benefits them, and of course others who oppose repeal for various reasons. A mixture model might be able to separate these different groups more effectively than can be done using simple regressions.

Daniel Ho, Kosuke Imai, Gary King, and Liz Stuart recently wrote a paper on matching, followed by regression, as a tool for causal inference. They apply the methods developed by Don Rubin in 1970 and 1973 to some political science data, and make a strong argument, both theoretical and practical, for why this approach should be used more often in social science research.

I read the paper, and liked it a lot, but I had a few questions about how it "sold" the concept of matching. Kosuke, Don, and I had an email dialogue including the following exchange.

[The abstract of the paper claims that matching methods "offer the promise of causal inference with fewer assumptions" and give "considerably less model-dependent causal inferences"]

AG: Referring to matching as "nonparametric and non-model-based" might be misleading. It depends on how you define "model", I guess, but from a practical standpoint, information has to be used in the matching, and I'm not sure there's such a clear distinction between using a "model" as compared to an "algorithm" to do the matching.

DR: I think much of this stuff about "models" and non-models is unfortunate. Whatever procedure you use, you are ignoring certain aspects of the data (and so regarding them as irrelevant), and emphasizing aspects as important. For a trivial example, when you do something "robust" to estimate the "center" of a distn, you are typically making assumptions about the definition of "center" and the irrelevance of extreme observations to the estimation of the it. Etc.

KI: I want to take this opportunity and ask you one quick question. When I talk about matching methods to political scientists who are so used to running a bunch of regressions, they often ask why matching is better than regression or why they should bother to do matching in combination with regressions. What would be the best way to answer this question? I usually tell them about the benefits of the potential outcome framework, available diagnostics, and flexibility (e.g., as opposed to linear regression) etc. But, I'm wondering what you would say to social scientists!

AG: Matching restricts the range of comparison you're doing. It allows you to make more robust inferences, but with a narrower range of applicability. See Figure 7.2 on page 227 of our book for a simple picture of what's going on, in an extreme case. Matching is just a particular tool that can be used to study a subset of the decision space. The phrase I would use for social scientists is, "knowing a lot about a little". The papers by Dehejia and Wahba discuss these issues in an applied context: http://www.columbia.edu/%7Erd247/papers/w6586.pdf and http://www.columbia.edu/%7Erd247/papers/matching.pdf

DR: Also look at the simple tables in Cochran and Rubin (1973) or Rubin (1973) or Rubin (1979) etc. They all show that regression by itself is terribly unreliable with minor nonlinearity that is difficult to detect, even with careful diagnostics. This message is over three decades old!

KI: I agree that matching gives more robust inferences. That's the main message of the paper that I presented and also of my JASA paper with David. The question my fellow social scientists ask is why matching is more robust than regressions (and hence why they should be doing matching rather than running regressions). One answer is that matching removes some observations and hence avoids extrapolation. But how about other kinds of matching that use all the observations (e.g., subclassification and full matching)? Are they more robust than regressions? What I usually tell them is that regressions often make stronger functional form assumptions than matching. With stratification, for example, you can fit separate regressions within each strata and then aggregate the results (therefore it does not assume that the same model fits all the data). I realize that there is no simple answer to this kind of a vague, and perhaps illposed, question. But, these are the kind of questions that you get when you tell soc. sci. about matching methods!

AG: I think the key idea is avoiding extrapolation, as you say above. But I don't buy the claim that regression makes stronger functional form assumptions than matching. Regressions can (and should) include interactions. Regression-with-interaction, followed by poststratification, is a basic idea. It can be done with or without matching.

The social scientists whom I respect are more interested in the models than in the estimation procedures. For these people, I would focus on your models-with-interactions. If matching makes it easier to fit such models, that's a big selling point of matching to me.

KI: One can think of it as a way to fit models with interactions in the multivariate setting by helping you create matches and subclasses. One thing I wanted to emphasize in my talk is that matching is not necessary a substitute for regressions, and that one can use matching methods to make regressions perform more robust.

Op/Ed from USA Today (10/28/04)

Are the unsteady poll numbers making you queasy? Me, too. But now, a team led by a Columbia University professor has figured out why the Bush-Kerry pre-election polls have jumped around so much.

The polls are trying to capture two moving targets at the same time, and that multiplies the motion. One target is presidential choice. The other, more difficult one, is the composition of the actual electorate — the people who will exercise their right to vote.

While it is a pretty good bet that more than half of the voting-age population will turn out on Nov. 2 (or before, in states that allow early voting), nobody knows for sure who will be in that active half. A study led by Robert Erikson of Columbia's department of political science analyzed data from Gallup's daily tracking polls in the 2000 election and found that the tools for predicting voter participation are even more uncertain than the tools for identifying voter choice.

With every fresh poll, people move in and out of the likely-voter group, depending on who is excited by the news of the day. Only now, this close to the election, can we expect the likely-voter group to stop gyrating and settle down.

This is why predicting elections is the least useful application of early pre-election polls. They ought to be used to help us see what coalitions are forming in the electorate, help us understand why the politicians are emphasizing some issues and ducking others. None of that can be done if the measures are unstable.

Years ago, when George Gallup and Louis Harris dominated the national polling scene, pre-election polls focused on the voting-age population and zeroed in on the likely voters only at the last minute.

This year, the likely-voter model kicked in for the USA TODAY/CNN/Gallup Poll with the first reading in January. News media reported both numbers — the likely-voter and the registered-voter choices. But the more volatile likely-voter readings got the most play.

The volatility may be newsworthy, but it's artificial. Erikson and his colleagues point out that most of the change in support for President Bush "is not change due to voter conversion from one side to the other but rather, simply, changes in group composition."

Who are the likely voters?

The decision on who belongs in the likely-voter group is made differently by different pollsters. Gallup, which has done this the longest, uses eight questions, including, "How much thought have you given to the upcoming elections, quite a lot or only a little?"

Responses to these questions tend to "reflect transient political interest on the day of the poll," said Erikson and his co-authors in an article scheduled for a forthcoming issue of Public Opinion Quarterly. That transient interest bobs up and down with the news and creates short-lived effects on the candidate choices. "Observed differences in the preferences of likely and unlikely voters do not even last for three days," the scholars reported. "They can hardly be expected to carry over to Election Day."

So what are the polls for?

A likely-voter poll is the right thing to do if all you want is to predict the outcome of the election — but that's a nonsensical goal weeks before the event. Campaigns change things. That's why we have them.

It would be far more useful to democracy if polls were used to see how the candidates' messages were playing to a constant group, such as registered voters or the voting-age population. Whoever is elected will, after all, represent all of us.

Behind all of the campaign hoopla is a determined effort by each party to organize a majority coalition. Polls, properly used and interpreted, could illuminate that process.

For example, a key question in this campaign is the stability of the low-to-middle income groups that have been voting Republican. They are subject to switching because they are tugged by GOP social issues, such as abortion and gay marriage, on one side and by their economic interests, such as minimum wage, health care and Social Security, on the other.

The polls produce that kind of information, but we are blinded to it because the editors and headline writers like to fix on the illusory zigzags in the horse race.

Scoreboard shouldn't block field of play

Some critics argue that media should stop reporting the horse-race standings. That solution is too extreme. A game wouldn't be nearly as interesting without a scoreboard. But a game where we can't see what the players are doing because the scoreboard blocks our view would not be much fun, either.

We are now close enough to the election for the likely-voter models to settle down and start making more sense. Expect the polls to start converging in the next few days, and they will probably be about as accurate as they usually are.

In the 17 presidential elections since 1936, the Gallup poll predicted the winner's share of the popular vote within two percentage points only six times. But it was within four points in 13 of the 17. It ought to do at least that well this time.

Philip Meyer is a Knight Professor of Journalism at the University of North Carolina at Chapel Hill. He also is a member of USA TODAY's board of contributors. His next book, The Vanishing Newspaper: Saving Journalism in the Information Age, will be published in November.

The phrase "curse of dimensionality" has many meanings (with 18800 references, it loses to "bayesian statistics" in a googlefight, but by less than a factor of 3). In numerical analysis it refers to the difficulty of performing high-dimensional numerical integrals.

But I am bothered when people apply the phrase "curse of dimensionality" to statistical inference.

In statistics, "curse of dimensionality" is often used to refer to the difficulty of fitting a model when many possible predictors are available. But this expression bothers me, because more predictors is more data, and it should not be a "curse" to have more data. Maybe in practice it's a curse to have more data (just as, in practice, giving people too much good food can make them fat), but "curse" seems a little strong.

With multilevel modeling, there is no curse of dimensionality. When many measurements are taken on each observation, these measurements can themselves be grouped. Having more measurements in a group gives us more data to estimate group-level parameters (such as the standard deviation of the group effects and also coefficients for group-level predictors, if available).

In all the realistic "curse of dimensionality" problems I've seen, the dimensions--the predictors--have a structure. The data don't sit in an abstract K-dimensional space; they are units with K measurements that have names, orderings, etc.

For example, Marina gave us an example in the seminar the other day where the predictors were the values of a spectrum at 100 different wavelengths. The 100 wavelengths are ordered. Certainly it is better to have 100 than 50, and it would be better to have 50 than 10. (This is not a criticism of Marina's method, I'm just using it as a handy example.)

For an analogous problem: 20 years ago in Bayesian statistics, there was a lot of struggle to develop noninformative prior distributions for highly multivariate problems. Eventually this line of research dwindled because people realized that when many variables are floating around, they will be modeled hierarchically, so that the burden of noninformativity shifts to the far less numerous hyperparameters. And, in fact, when the number of variables in a a group is larger, these hyperparameters are easier to estimate.

I'm not saying the problem is trivial or even easy; there's a lot of work to be done to spend this blessing wisely.

This is the reference to the work of Chipman on including interactions: Chipman, H. (1996), ``Bayesian Variable Selection with Related Predictors'', Canadian Journal of Statistics , 24, 17--36.

The following is from Marina Vannucci, who will be speaking in the Bayesian working group on Oct 26.

I will briefly review Bayesian methods for variable selection in regression settings. Variable selection pertains to situations where the aim is to model the relationship between a specific outcome and a subset of potential explanatory variables and uncertainty exists on which subset to use. Variable selection methods can aid the assessment of the importance of different predictors, improve the accuracy in prediction and reduce cost in collecting future data. Bayesian methods for variable selection were proposed by George and McCulloch (JASA,1993). Brown, Vannucci and Fearn (1998, JRSSB) generalized the approach to the case of multivariate responses. The key idea of the model is to use a latent binary vector to index the different possible subsets of variables (models). Priors are then imposed on the regression parameters as well as on the set of possible models. Selection is based on the posterior model probabilities, obtained, in principle, by Bayes theorem. When the number of possible models is too large (with p predictors there are 2^p possible subsets) Markov chain Monte Carlo (MCMC) techniques can be used as stochastic search techniques to look for models with high posterior probability. In addition to providing a selection of the variables, the Bayesian approach allows model averaging, where prediction of future values of the response variable is computed by averaging over a range of likely models.

I will describe extensions to multinomial probit models for simultaneous classification of the samples and selection of the discriminatory variables. The approach taken makes use of data augmentation in the form of latent variables, as proposed by Albert and Chib (JASA,1993). The key to this approach is to assume the existence of a continuous unobserved or latent variable underlying the observed categorical response. When the latent variable crosses a threshold, the observed category changes. A linear association is assumed between the latent response, Y, and the covariates X. I will again consider the case of a large number of predictors and applied Bayesian variable selection methods and MCMC techniques. An extra difficulty here is represented by the latent responses, which is treated as missing and imputed from marginal truncated distributions. This work in published in see Sha, Vannucci et al. (Biometrics,2004). I have put a link to the paper from the group webpage.

In a multi-way analysis of variance setting, the number of possible predictors can be huge. For example, consider a 10x19x50 array of continuous measurements, there is a grand mean, 10+19+50 main effects, 10x19+19x50+10x50 two-way interactions. and 10x19x50 three-way interactions. Multilevel (Bayesian) anova tools can be used to estimate the scales of each of these batches of effects and interactions, but such tools treat each batch of coefficients as exchangeable.

But more information is available in the data. In particular, factors with large main effects tend to be more likely to have large interactions. From a Bayesian point of view, a natural way to model this pattern would be for the variance of each interaction to depend on the coefficients of its component parts.

A model for two-way data

For example, consider a two-way array of continuous data, modeled as y_ij = m + a_i + b_j + e_ij. The default model is e_ij ~ N(0,s^2). A more general model is e_ij ~ N(0,s^2_ij), where the standard deviation s_ij can depend on the scale of the main effects; for example, s_ij = s exp (A|a_i| + B|b_j|).

Here, A and B are coefficients which would have to be estimated from the data. A=B=0 is the standard model, and positive values of A and B correspond to the expected pattern of larger main effects having larger interactions. (We're enclosing a_i and b_j in absolute values in the belief that large absolute main effects, whether positive or negative, are important.)

We fit this model to some data (on public spending by state and year) and found mostly positive A's and B's.

The next step is to try the model on more data and to consider more complicated models for 3-way and higher interactions.

Why are we doing this?

The ultimate goal is to get better models that can allow deep interactions and estimate coefficients without requiring that entire levels of interactions (e.g., everything beyond 2-way) be set to zero.

An example of an applied research problem where we struggled with the inclusion of interactions is the study of the effects of incentives on response rates in sample surveys. Several factors can affect response rate, including the dollar value of the incentive, whether it is a gift or cash, whether it is given before or after the survey, whether the survey is telephone or face-to-face, etc. One could imagine estimating 6-way interactions, but with the available data it's not realistic even to include all the three-way interactions. In our analysis, we just gave up and ignored high-level interactions and kept various lower-level interactions based on a combination of data analysis and informal prior information but we'd like to do better.

Jim Hodges and Paul Gustafson and Hugh Chipman and others have worked on Bayesian interaction models in various ways, and I expect that in a few years there will be off-the-shelf models to fit interactions. Just as hierarchical modeling itself used to be considered a specialized method and is now used everywhere, I expect the same for models of deep interactions.

Hi all,

Does anybody know how to do 2-stage (or 3-stage) least squares regression in Stata? I'm trying to replicate Shepherd's analysis on her dataset, and running into problems.

I think my specific problem is that she estimates 50 different execution parameters (state-specific deterrence effects), so when I try and run this, I'm finding that "the system is not identified", which I'm assuming means that there are too many endogenous predictors and not enough instruments.

If anyone had any advice (specifically on how to do this with a system of 4 equations, not in reduced form -- I'm currently using the reg3 command), that'd be great. I'm going out of town so I'll miss this Friday's seminar, but any ideas would be most appreciated.

Thanks!

The following is from Sampsa Samila, who will be speaking in the quantitative political science working group on Fri 12 Nov.

The general context is the venture capital industry. What I [Sampla Samila] am thinking is to specify a location for each venture capital firm in a "social space" based on the geographic location and the industry of the companies in which it invests. So the space would have a geographic dimension and an industry dimension and each venture capital firm's position would be a vector of investments falling in different locations in this space. (There might be a futher dimension based on which other venture capital firms it invests, the network of co-investments.)

The statistical problem then is to assess how much of the movement of a particular venture capital firm in this space is due to the locations of other venture capital firms in this space (do they attract or repel each other and under what conditions?) and how much is due to the success of investments in particular geographic areas and industries (the venture capital firms are generally likely to invest where there are high-quality companies to invest in). Other factors would include the geographic location of the venture capital firm itself and its co-investments with other venture capital firms. In mathematical terms, the problem is to estimate how the characteristics of different locations and the positions of others influence the vector of movement (direction and magnitude). One could also look at where in this space do new venture capital firms appear and in which locations are venture capital firms most likely to fail.

One possible problem could be that the characteristics of the space also depend on the location of the firms. That is, high-quality companies are likely to be established where they have resources and high-quality venture capital is one of them.

The sociological contributions of this project would be to study:

1) the dynamics of competition and legitimation (the benefits one firm gets from being close to a other firms versus the downside of it)

2) the dynamics of social comparison (looking at how success/status differentials between venture capital firms affect whether they attract or repel each other, one can also look at which one moves closer or futher away from the other)

3) clustering of firms together.

Any thoughts?

Introduction

In recent US presidential elections we have observed, at the macro-level, that higher-income states support Democratic presidential candidates (eg, California, New York,) and lower-income states support Republcan presidential candidates (eg, Alabama, Mississippi). However, at the micro-level, we observe that higher-income voters support Republican presidential candidates, and lower-income voters support Democratic presidential candidates. What explains this apparent paradox?

Journalistic Explanation

Journalists seem to argue with the second half of the paradox, namely, higher-income voters support Republican presidential candidates, and lower-income voters support Democratic presidential candidates.

Brooks (2004) points out that a large class of affluent professionals are solidly Democratic. Specifically, he notes that 90 out of 100 zip codes where the median home income was above $500,000 elected liberal Democrats.

Barnes (2002) find that 38% of voters in "strong Bush" counties had household incomes below $30,000, while 7% earned only $100,000; and 29% of voters in "strong Gore" counties had household incomes below $30,000, while 14% was above $100,000.

Wasserman (2002) also finds similar trends. Per capital income in "Blue" states was $28,000 vs. $24,000 for "Red" states. Eight of the top 10 metropolitan areas with the highest per capital income were from "Blue" states; and 8 of the top 10 metropolitan areas with the lowest income levels were from "Red" states.

The journalistic explanation is that higher-income individuals, and as a result, wealthly areas are Democratic; and lower-income individuals, and as a result, lower-income areas are Republican. Therefore, journalists would argue that there is no paradox.

Are Journalists Right?

McCarty, et al. (2003) in their examination of political polarization and income inequality show that partisanship and presidential vote choice have become more stratified by income. It was true that income was not a reliable predictor of political beliefs and partisanship in the mass public. Partisanship was only weakly related to income in the period following World War II. According to McCarty et al. (2003), in the presidential elections of 1956 and 1960, respondents from the highest quintile were hardly more likely to identify as a Republican than respondents from the lowest quintile. However, elections of 1992 and 1996, respondents in the highest quintile were more than twice as likely to identify as a Republican than were those in the lowest quintile.

If the Journalists are Wrong, What Explains the Paradox?

One possible explanation. Lower-income individuals in higher-income states turnout in higher rates; and higher-income individuals in lower-income states turnout in higher rates producing the Red State/Blue State paradox. In short, an aggregation problem.

So how do we prove this? To be continued...

Here's a fun demonstration for intro statistics courses, to get the students thinking about random sampling and its difficulties.

As the students enter the classroom, we quietly pass a sealed envelope to one of the students and ask him or her to save it for later. Then, when class has begun, we pull out a digital kitchen scale and a plastic bag full of a variety of candies of different shapes and sizes, and we announce:

This bag has 100 candies, and it is your job to estimate the total weight of the candies in the bag. Divide into pairs and introduce yourself to your neighbor. [At this point we pause and walk through the room to make sure that all the students pair up.] We're going to pass this bag and scale around the room. For each pair, estimate the weight of the 100 candies in the bag, as follows: Pull out a sample of 5 candies, weigh them on the scale, write down the weight, put them candies back in the bag and mix them (no, you can't eat any of them yet!), and pass the bag and scale to the next pair of students. Once you've done that, multiply the weight of your 5 candies by 20 to create an estimate for the weight of all 100 candies. Write that estimate down (silently, so as not to influence the next pair of students who are taking their sample). [As we speak, we write these instructions as bullet points on the blackboard: "Draw a sample of 5," "Weigh them," etc.]

Your goal is to estimate the weight of the entire bag of 100 candies. Whichever pair comes closest gets to keep the bag. So choose your sample with this in mind.

We then give the bag and scale to a pair of students in the back of the room, and the demonstration continues while the class goes on. Depending on the size of the class, it can take 20 to 40 minutes. We just cover the usual class material during this time, keeping an eye out occasionally to make sure the candies and the scale continue to move around the room.

When the candy weighing is done (or if only 15 minutes remain in the class), we continue the demonstration by asking each pair to give their estimate of the total weight, which we write, along with their first names, on the blackboard. We also draw a histogram of the guesses, and we ask whether they think their estimates are probably too high, too low, or about right.

We then pass the candies and scale to a pair of students in front of the class and ask them to weigh the entire bag and report the result. Every time we have done this demonstration, whether with graduate students or undergraduates, the true weight is much lower than most or all of the estimates---so much lower that the students gasp or laugh in surprise. We extend the histogram on the blackboard to include the true weight, and then ask the student to open the sealed envelope, and read to the class the note we had placed inside, which says, "Your estimates are too high!"

We conclude the demonstration by leading a discussion of why their estimates were too high, how they could have done their sampling to produce more accurate estimation, and what analogies can they draw between this example and surveys of human populations. When students suggest doing a "random sample," we ask how they would actually do it, which leads to the idea of a sampling frame or list of all the items in the population. Suggestions of more efficient sampling ideas (for example, picking one large candy bar and four smaller candies at random) lead to ideas such as stratified sampling.

---

When doing this demonstration, it's important to have the students work in pairs so that they think seriously about the task.

It's also most effective when the candies vary greatly in size: for example, take about 20 full-sized candy bars, 30 smaller candy bars, and 50 very small items such as individually-wrapped caramels and Life Savers.

I read that Morris Fiorina will discuss the culture war in America this Sun at 5:15pm on C-SPAN. He may talk about Red/Blue states.

Culture War?: The Myth of a Polarized America by Morris Fiorina

Description: Morris Fiorina challenges the idea that there is a culture war taking place in America. Mr. Fiorina argues that while both political parties and pundits the country is constantly present the country as being divided, the reality is that most people hold middle-of-the-road views on almost all of the major issues. The talk was hosted by Stanford University's Hoover Institution.

Author Bio: Morris Fiorina is a senior fellow at the Hoover Institution and a professor of political science at Stanford University. His books include "The New American Democracy" and "The Personal Vote: Constituency Service and Electoral Independence."

Publisher: Pearson Longman 1185 Avenue of the Americas New York, NY 10036

Introduction

Heterogeneous choice model allows researchers to model the variance of individual level choices. These models have their roots in heteroskedasticity (unequal variance) and the problems it creates for statistical inference. In the context of linear regression, unequal variance does not bias the estimates, rather it inflates or underestimates the true standard errors in the model. Unequal variance is more problematic in discrete choice models, such as logit or probit (and their ordered or multinomial variants). If we have unequal variances in the error term of a discrete choice model, not only are the standard errors incorrect, but the parameters are also biased.

Example

The classic political science example involves ambivalence and value conflict. Alvarez and Brehm (1995) modeled the variation in responses to survey questions on abortion to demonstrate that this variation results not from respondents offering ill-informed opinions, but instead is a product of the ambivalence that results from wrestling with a difficut and important choice. This is a case where the variability in the choice is actually more interesting than what determines the choice.

Estimation

Estimation of heterogeneous choice models is fairly straightforward. A researcher that suspects heterogeneous choices can select a set of covariates and model the heterogeneity. However, the properties of these models are not well understood. There is little analytical or empirical evidence how well these models perform.

Monte Carlo Experiments

Using monte carlo experiments, we examine how well these models estimate the parameters used to make inferences about heterogeneous choices. We find that these models are deeply flawed. Not only are these model an ineffective "cure" for heteroskedasticity, the estimates of these models are biased and provide incorrect estimates of the standard errors.

The estimated sampling variability and coverage rates were less than ideal even under a perfect specification. Measurement error in the variance model induced significant amounts of bias, and almost any specification error causes the estimates of both the choice and variance model to be completely unreliable. Even in models where teh variable used to estimate the choice was correlated with the true variable at 0.90, all the parameters were estimated very poorly, being biased by over 60%. And, it is entirely possible to misspecify both the choice and variance model, which should only make the estimates worse.

Conclusion

Of course it is easier to tear down than to build up. To that end, we intend to devise an alternative way to model heterogeneous choices. Bayesian estimation techniques offers such a possibility, with its focus on the variance of all parameters. Such an approach should give us better leverage over the heterogeneity of individual choices

David Samuels of the University of Minnesota, who coauthored a paper with Richard Snyder in 2001 on unequal representation for the British Journal of Political Science ("The Value of a Vote: Malapportionment in Comparative Perspective"), had some helpful comments on our post on overrepresentation of small states/provinces:

Check out Thies' work on the consequences of over-representation in Japan, if you haven't seen it already. A paper that appears in the last year in LSQ by two Japanese political scientists (and that won an award from the Legis. Studies section of APSA) was on the same subject and country.

Edward Gibson's work (and with former grad students - articles in World Politics, etc.) has looked at the consequences of apportionment distortions in Latin America for fiscal policy, e.g. My book, published last year, looks at the relationship between federalism and executive-legislative relations in Brazil, with particular attention to malapportionment of under-populated states. Federalism and Territorial Politics in Latin America.

I'd also again say that the piece Rich and I have in Gibson's edited volume (Federalism and Territorial Politics in Latin America) might be good food for thought for you as for causal stories. For example, in Latin America the key political dynamic that *generated* malapportionment was not federalism per se (the case of Chile bears this out quite clearly), but that both authoritarian and democratic leaders have sought to manipulate the "rules of representation" to favor their allies. This includes forgoing a decennial census, which has the effect of under-representing any city experiencing population growth over time (Chile), creating 2 new states out of 1 old state (Argentina, Brazil), etc. etc. The US seems unique, or close to it, in that the court system has imposed a 1-person 1-vote solution in the lower chamber of the legislature. In some countries, e.g. the UK, political negotiations lead to a similar outcome (e.g. the last Reform Act), but in many countries, it seems that political-electoral concerns favoring under-represented districts overwhelm lofty democratic notions of the equality of the weight of the vote for all citizens - even in single-chamber legislatures in non-federal systems.

Good luck,
David

Just a quick note on what we're doing with Shepherd's paper, and why...

There's a long standing economics literature (beginning with Ehrlich in 1975) on the question of whether the death penalty deters murders. Since the death penalty is used in some states and not others, and has been used to differing extents over the years, it tends to be treated as a natural experiment.

However, capital punishment is not implemented at random -- be it the political climate, current crime rates, or inherent differences across states, there's something that drives some states to legalize the death penalty, and others not to. Furthermore, the "deterrent effect" of the death penalty varies by state and time, making it difficult to make a single causal claim of deterrence or the lack thereof.

Since there are such differences across states and time, the question of deterrence may lend itself to a multilevel model. Most modern papers look at data by state and year, and a multilevel model allows some flexibility in the appropriate level of aggregation.

Joanna Shepherd's recent paper (available on the Wiki) uses a series of equations to predict murder rates by county and year, as a function of deterrent (and other) measures, and predict the probabilities of arrest, death sentences, and executions, based on murder rates and a number of other factors.

She finds that in some states, executions "deter" crime, in others there is no effect, and in still others, executions "cause" crime. We plan to test the sensitivity of these findings to changes in model specifications.

We don't have her data yet; at the moment I'm using Stata to play with some state-level data to try and get a handle on her model. The county-by-year data might add more to a multilevel model than state-level data, since the death penalty is legalized by state, but deterrent effects may be felt more locally.

We're also planning to test some of the other model specifications -- the reliance on publicity, differences between high-execution and low-execution states, and so forth.

I'm meeting with Jeff on Friday, who has some ideas of what we should be testing, and will relay that conversation...

It is well known that states are overrepresented in the U.S. political system. For example, Wyoming has 0.2% of the U.S. population but has 0.6% of the Electoral College votes for President, and 2% of the U.S. senators; while California has 12% of the population, 10% of the electoral votes, and still only 2% of the senators. To put it another way: Wyoming has 6 electoral votes and 2 senators per million voters, while California has 1.5 electoral votes and 0.06 senators per million voters. There is also a disparity in federal funding; for example, Wyoming received $7200 and California only $5600 in direct federal spending per capita in 2001.

On the whole, the disparity in the Electoral College is pretty minor, but the U.S. Senate disparity is huge: the 21 smallest states have the population of California but 42 Senators compared to California's two.

Other countries too

We have looked at other countries (Mexico, Canada, Japan, Argentina, Thailand, . . .) and found similar patterns: smaller states (provinces) have more legislative representatives per capita and more spending per capita.

For any country, we can summarize the relationship of representation and population by making a graph, with one dot per state (province), plotting the logarithm of #representatives per capita on the y-axis, and the logarithm of population on the x-axis. The graph typically has a negative slope: larger states within a country tend to have fewer representatives per person.

We then fit a regression line to the data and summarize it by the slope. A slope of 0 is complete fairness with respect to population size: neither small nor large states get more per-capita representation. A slope of -1 is like the U.S. Senate, with a huge imbalance in representation per person. A positive slope would imply that voters in large states are actually overrepresented.

What do the data look like? Slopes are typically negative, ranging from 0 down to -1. Small states consistently get more representatives per person.

Similarly, we make graphs of log(federal spending per capita) vs. log(population) for the states in each country, and we find negative slopes throughout. Typical slopes are between -0.2 and -0.5, so that small states get more funding per person--no surprise, given their overrepresentation.

Why do we care?

Well, it seems unfair, violating the "one-person, one-vote" norm. The spending inequalities represent real money. Also, it's interesting to see such a strong pattern. If it only occurred in U.S., we'd wonder what was special about our system. Since the small-state bias seems to occur all over, we wonder what general features of political systems make it possible.

How did it happen and how does it persist?

There are lots of possible stories. In countries such as the United States that formed from federations, the small states had some bargaining power in the constitution-writing process. (It has been pointed out, however, that the ratio between the largest and smallest state populations has increased greatly over the lifetime of the U.S.) Similarly, small states have some veto power in the European Union, which may have help explain how they have achieved their overrepresentation in the Council of Ministers.

Small states tend to be more rural and have larger land areas per person, both of which may be sources for federal spending (although this wouldn't explain the overrepresentation).

The USA Today effect

Another set of reasons for inequality to persist is if it's not recognized as such. Suppose we were to think of states as persons. Then it makes sense to give each state an equal number of Senators--that's equal representation, right? From an individualist standpoint, this sounds silly, but in many contexts, the states are presented as equals.

For example, USA Today has a feature with news from each of the 50 states. There are a lot more people in Los Angeles or Chicago than in several of the smallest states, but they manage to find an equal-length snippet from each. It's not always easy! For example, here's Idaho's entry for today, October 15:

Post Falls - Families are protesting the periodic removal of mementos they place on graves at the Evergreen Cemetery. The items include ceramic angels, American flags and baby bracelets. Cemetery sexton Bob Harvego says the city must keep the graves tidy and that the mementos are stored.

A cognitive illusion

To think of it another way, California has 12% of the U.S. population. Suppose it were overrepresented and get 40% of the Senators. It would bother people that almost every other Senator is from California--it would just seem weird, and it would be clear that the state is overrepresented. But, here in the real world, the 21 smallest states--whose total population is less than California's--get 42 senators, people don't seem to mind that! These small states have different names, so their overrepresentation is not so obvious.

[no link to a paper here; megumi and the rest of us are still working on the paper summarizing the empirical results and possible explanations]

P.S. See here and here for a partisan take on this issue.

Is statisticsl inference inductive or deductive reasoning? What is the connection between statistics and the philosophy of science? Why do we care?

The usual story

Schools of statistical inference are sometimes linked to philosophical approaches. "Classical" statistics--as exemplified by Fisher's p-values and Neyman's hypothesis tests--is associated with a deductive, or Popperian view of science: a hypothesis is made and then it is tested. It can never be accepted, but it can be rejected (that is, falsified).

Bayesian statistics--starting with a prior distribution, getting data, and moving to the posterior distribution--is associated with an inductive approach of gradually moving forward, generalizing from data to learn about general laws as expressed in the probability that one model or another is correct.

Our story

Our progress in applied modeling has fit the Popperian pattern pretty well: we build a model out of available parts and drive it as far as it can take us, and then a little farther. When the model breaks down, we take it apart, figure out what went wrong, and tinker with it, or else try a radically new design. In either case, we are using deductive reasoning as a tool to get the most out of a model, and we test the model--it is falsifiable, and when it is falsified, we alter or abandon it. To give this story a little Kuhnian flavor, we are doing "normal science" when we apply the deductive reasoning and learn from a model, or when we tinker with it to get it to fit the data, and occasionally enough problems build up that a "new paradigm" is helpful.

OK, all fine. But the twist is that we are using Bayesian methods, not classical hypothesis testing. We do not think of a Bayesian prior distribution as a personal beliefs; rather, it is part of a hypothesized model, which we posit as potentially useful and abandon to the extent that it is falsified.

Subjective Bayesian theory has no place for falsification of prior distributions--how do you falsify a belief? But if we think of the model just as a set of assumptions, they can be falsified if their predictions--our deductive inferences--do not fit the data.

Why does this matter?

A philosophy of deductive reasoning, accompanied by falsifiability, gives us a lot of flexibility in modeling. We do not have to worry about making our prior distributions match our subjective knowledge, or about our model containing all possible truths. Instead we make some assumptions, state them clearly, and see what they imply. Then we try to falsify the model--that is, we perform posterior predictive checks, creating simulations of the data and comparing them to the actual data. The comparison can often be done visually; see chapter 6 of Bayesian Data Analysis for lots of examples.

I associate this "objective Bayes" approach--making strong assumptions and then testing model fit--to the work of E. T. Jaynes. As he has illustrated, the biggest learning experience can occur when we find that our model does not fit the data--that is, when it is falsified--because then we have found a problem with our underlying assumptions.

Conversely, a problem with the inductive philosopy of Bayesian statistics--in which science "learns" by updating the probabilities that various competing models are true--is that it assumes that the true model is one of the possibilities being considered. This can does not fit our own experiences of learning by finding that a model doesn't fit and needing to expand beyond the existing class of models to fix the problem.

I fear that a philosophy of Bayesian statistics as subjective, inductive inference can encourage a complacency about picking or averaging over existing models rather than trying to falsify and go further. Likelihood and Bayesian inference are powerful, and with great power comes great responsibility. Complex models can and should be checked and falsfied.

Postscript

These ideas are also connected to exploratory data analysis
(see this paper in the International Statistical Review).

Also, Sander Greenland has written on the philosophy of Bayesian inference from a similar perspective--he has less sympathy with Popperian terminology but similarly sees probabilistic inference within a model as deductive ("Induction versus Popper: substance versus semantics" in International Journal of Epidemiology 27, 543-548 (1998).)

The chance that your vote will be decisive in the Presidential election is, at best, about 1 in 10 million. So why vote?

Schematic cost-benefit analysis

To express formally the decision of whether to vote:

U = p*B - C, where

U = the relative utility of going and casting a vote
p = probability that, by voting, you will change the election outcome
B = the benefit you would feel from your candidate winning (compared to the other candidate winning)
C = the net cost of voting

The trouble is, if p is 1 in 10 million, then for any reasonable value of B, the product p*B is essentially zero (for example, even if B is as high as $10000, p*B is 1/10 of one cent), and this gives no reason to vote.

The usual explanation

Actually, though, about half the people vote. The simplest utility-theory explanation is that the net cost C is negative for these people--that is, the joy of voting (or the satisfying feeling of performing a civic duty) outweighs the cost in time of going out of your way to cast a vote.

The "civic duty" rationale for voting fails to explain why voter turnout is higher in close elections and in important elections, and it fails to explain why citizens give small-dollar campaign contributions to national candidates. If you give Bush or Kerry $25, it's not because you're expecting a favor in return, it's because you want to increase your guy's chance of winning the election. Similarly, the argument of "it's important to vote, because your vote might make a difference" ultimately comes down to that number p, the probability that your vote will, in fact, be decisive.

Our preferred explanation

We understand voting as a rational act, given that a voter is voting to benefit not just himself or herself, but also the country (or the world) at large. (This "social" motivation is in fact consistent with opinion polls, which find, for example, that voting decisions are better predicted by views on the economy as a whole than by personal financial situations.)

In the equation above, B represents my gain in utility by having my preferred candidate win. If I think that Bush (or Kerry) will benefit the country as a whole, then my view of the total benefit from that candidate winning is some huge number, proportional to the population of the U.S. To put it (crudely) in monetary terms, if my candidate's winning is equivalent to an average $100 for each person (not so unreasonable given the stakes in the election), then B is about $30 billion. Even if I discount that by a factor of 100 (on the theory that I care less about others than myself), we're still talking $300 million, which when multiplied by p=1/(10 million) is a reasonable $30.

Some empirical evidence

As noted above, voter turnout is higher in close elections and important elections. These findings are consistent with the idea that it makes more sense to vote when your vote is more likely to make a difference, and when the outcome is more important.

As we go from local, to state, to national elections, the size of the electorate increases, and thus the probability decreases of your vote being decisive, but voter turnout does not decrease. This makes sense in our explanation because national elections affect more people, thus the potential benefit B is multiplied by a larger number, canceling out the corresponding decrease in the probability p.

People often vote strategically when they can (in multicandidate races, not wanting to "waste" their votes on candidates who don't seem to have a chance of winning). Not everyone votes strategically, but the fact that many people do is evidence that they are voting to make a difference, not just to scratch an itch or satisfy a civic duty.

As noted above, people actually say they are voting for social reasons. For example, in the 2001 British Election Study, only 25% of respondents thought of political activity as a good way to get "benefits for me and my family" whereas 66% thought it a good way to obtain "benefits for groups that people care about like pensioners and the disabled."

Implications for voting

First, it can be rational to vote with the goal of making a difference in the election outcome (not simply because you enjoy the act of voting or would feel bad if you didn't vote). If you choose not to vote, you are giving up this small but nonzero chance to make a huge difference.

Second, if you do vote, it is rational to prefer the candidate who will help the country as a whole. Rationality, in this case, is distinct from selfishness.

See here for the full paper (joint work with Aaron Edlin and Noah Kaplan)

It is well known that the Electoral College favors small states: every state, no matter how small, gets at least 3 electoral votes, and so small states have more electoral votes per voter. This "well known fact" is, in fact, true.

To state this slightly more formally: if you are a voter in state X, then the probability that your vote is decisive in the Presidential election is equal to the probability that your vote is decisive within your state (that is, the probability that your state would be exactly tied without your vote), multiplied by the probability that your state's electoral votes are decisive in the Electoral College (so that, if your state flips, it will change the electoral vote winner), if your state were tied.

If your state has N voters and E electoral votes, the probability that your state is tied is approximately proportional to 1/N, and the probability that your state's electoral votes are necessary is approximately proportional to E. So the probability that your vote is decisive--your "voting power"--is roughly proportional to E/N, that is, the number of electoral votes per voter in your state.

A counterintuitive but wrong idea

The point has sometimes been obscured, unfortunately, by "voting power" calculations that purportedly show that, counterintuitively, voters in large states have more voting power ("One man, 3.312 votes," in the oft-cited paper of Banzhaf, 1968). This claim of Banzhaf and others is counterintuitive and, in fact, false.

Why is the Banzhaf claim false? The claim is based on the same idea as we noted above: voting power equals the probability that your state is tied, times the probability that your state's electoral votes are necessary for a national coalition. The hitch is that Banzhaf (and others) computed the probability of your state being tied as being proportional to 1/sqrt(N), where N is the number of voters in the state. This calculation is based (explicitly or implicitly) on a binomial distribution model, and it implies that elections in large states will be much closer (in proportion of the vote) than elections in small states.

Above is the result of the oversimplified model. In fact, elections in large states are only very slightly closer than elections in small states. As a result, the probability that your state's election is tied is pretty much proportional to 1/N, not proportional to 1/sqrt(N). And as a result of that, your voting power is generally more in small states than in large states.

Realistically . . .

Realistically, voting power depends on a lot more than state size. The most important factor is the closeness of the state. Votes in so-called "swing states" (Florida, New Mexico, etc.) are more likely to make a difference than in not-so-close states such as New York.

Above is a plot of "voting power" (the probability that your vote is decisive) as a function of state size, based on the 2000 election. These probabilities are based on simulations, taking the 2000 election and adding random state, regional, and national variation to simulate the uncertainty in state-by-state outcomes.

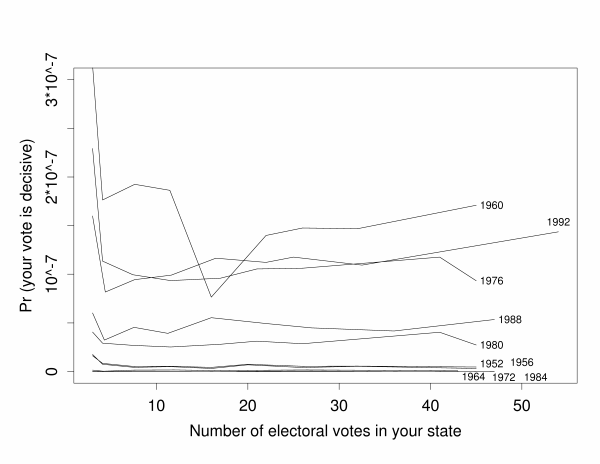
And above is a plot showing voting power vs. state size for a bunch of previous elections. These probabilities are based on a state-by-state forecasting model applied retroactively (that is, for each year, the estimated probability of tie votes, given information available before the election itself).

The punch line: you have more voting power if you live in a swing state, and even more voting power if you live in a small swing state. And, if you're lucky, your voting power is about 10^(-7), that is, a 1 in 10-million chance of casting a decisive vote.

Here's the full paper to appear in the British Journal of Political Science (joint work with Jonathan Katz and Joe Bafumi)

Go here for more details on the statistical models (joint work with Jonathan Katz and Francis Tuerlinckx)

Actually, though, it's still rational for you to vote, at least in many of the states.

In this weblog, we will report on recent research and ongoing half-baked ideas, including topics from our research groups on Bayesian statistics, multilevel modeling, causal inference, and political science. See Andrew Gelman's webpage for more background.

We will also post on anything that interests us that relates to statistical ideas and their applications.

Contributing to the blog will be Samantha Cook, Andrew Gelman, and various of Andrew's students and colleagues who would like to add things.

Comments will be helpful to suggest open problems, to point out mistakes in the work that we post, and to suggest solutions to some of the open problems we raise.