
Copyright (c) Aleks Jakulin,
2004. [e-mail] (remove
unnecessary dashes and spaces from the e-mail address to respond)
A. Jakulin, W. Buntine, T. M. La Pira and H. Brasher
Analyzing the U.S. Senate in 2003: Similarities, Clusters, and Blocs
Political Analysis (2009) 17 (3): 291-310.
[link]
A particular kind of data in politics that is well-amenable to data mining are the roll calls. In USA, the Library of Congress in Washington maintains the THOMAS database of legislative information for the US Senate and the US House of Representatives. We shall focus on the US Senate. For each roll call, the database provides a list of votes cast by each of the 100 senators. For each roll call, the vote of every senator is recorded in three ways: `Yea', `Nay' and `Not Voting'. A portion of the whole the table of issues debated in the US Senate then looks like this:
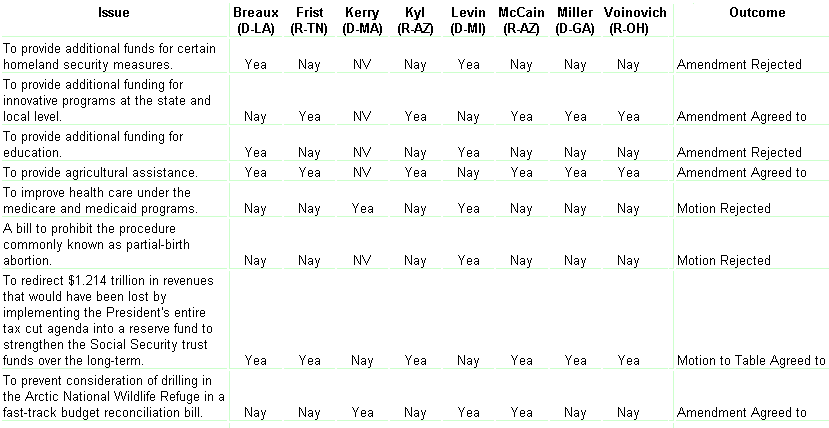
With this data we can do many interesting visualizations and analyses that will be discussed in the next section. We will learn how influential each senator is, how influential are individual states, which senators voted most similarly, and which blocs seem to exist in the US Senate. All this will be done purely and strictly from the data. There are many other domains with similar structure of the data: voting in other parliaments, such as the Finnish Eduskunta, voting in the United Nations, voting in the supreme courts, voting of shareholders, and so on.
The material in this section is a summary of the paper Analyzing the US Senate in 2003: Similarities, Networks, Clusters and Blocs listed beneath. We show that several methods often used in data mining, information theory and applied statistics are directly applicable to the roll call data, and are complementary to the methods already used in political science.
|
Clusters and Blocs in the Senate
The bars on the right hand side depict the five blocs resulting from latent variable analysis with Gibbs sampling, and the the darker blocks indicating a high degree of membership, the lighter ones a lower degree. The number of these blocs is subject to interpretation, but the assignment of senators to the blocs is much less ambiguous. With our statistical model, we identified five blocs: A: the majority Republican bloc, ~35 votes Each bloc can be interpreted as a single vote which is replicated several times, through its bloc members. Thereby, we can interpret a bloc as a single voting "super-senator", but with a weight proportional to the size of the bloc. It turns out that A and B are most influential, D does make an impact sometimes, and E quite rarely. Republican blocs, especially bloc B, were more cohesive than Democrat ones. |
||
|
A Similarity Matrix The symmetric dissimilarity matrix graphically illustrates the information-theoretic Rajski's distance between all pairs of senators, based on their votes in 2003. If two senators voted similarly, the square at the intersection of their names is dark. Three large clusters can be identified visually from this graph, and one group of moderate senators in each party. The major clusters correspond to the political parties even if the party information was not used in the computation of distance. Of interest is also Senator Kerry (D-MA) who is in the center of the Democrats while also being more similar than other Democrats to the Republicans: this can be achieved by not voting for every issue.
|
||
|
Similarity Networks Clustering does not illustrate the structure of strong similarities in detail. We can achieve this by plotting a graph with nodes corresponding to senators and edges to their connections. We only select a certain number of the strongest similarities to create a graph, using an artificial threshold to discriminate between a connection and the absence of it. We graphically illustrate the 20 pairs of senators with highest Rajski's distance between their votes, both in the Democratic and Republican Party. The nodes are labeled with the total number of votes cast, while the edges are marked with the percentage of roll calls in which both senators cast the same vote Among the Democrats, there is large variation in the number of votes cast, as those senators that later participated as candidates in the presidential race cast fewer votes than others, with Senator Kerry casting only 165 votes out of 459. This seemingly places him in the very center of the party. The closest pair among the Republican senators is formed by Senators Craig and Crapo, both from Idaho, who cast identical votes in 98.8% of cases. We also see the separation between the two Republican blocs.
|
||
|
How Influential is a Senator or a State? We can interpret the process of voting in the context of Shannon's information theory. Each senator can be considered as an information source, while the outcome of the vote is the destination. Therefore, mutual information can be interpreted as a measure of how influential is a senator with respect to the outcome of the vote. [How influential are individual senators?] It is also possible to consider both senators of a particular state as a joint information source. This way, we obtain the level of influence a particular state exerts on the outcome. [How influential are individual states?] In general, Republicans are considerably more influential than the Democrats, and relatively small states may be far more influential than populous states. The methods we employed were inspired by feature selection heuristics in machine learning.
|
||
|
|
Per-Issue Analysis It is possible to analyze the votes cast by blocs for each issue. There are several types of analysis that can be done:
|
|
|
Metric Scaling in 2D We have to distinguish similarity, which is in our case quantified information-theoretically with a probabilistic model, from distance that is defined geometrically. There are algorithms that attempt to present the similarities through distances, clarifying the similarity structure in data. The senators whose votes were similar, also appear close in the resulting diagrams. Instead of discrete clusters, we have implicit aggregations, groups of points. The colors are derived from bloc memberships in the latent variable model. The perceptual similarity of color marks the similarity based on the latent variable model.
|
||
|
Metric Scaling in 3D For viewing these files you need a VRML viewer or plug-in. Several methods are illustrated:
The colors are derived from bloc memberships. Hover the mouse over the ball, and you will obtain the name of the senator beneath it. All these methods yield relatively similar results, which can be seen as an indication that the findings are robust.
|
||
|
Belief Networks Belief nets provide a fascinating "causal" model of "influence" in the US Senate. It makes little sense. Do not play with causality! |
The methods merely illustrated above are explained in detail in our papers:
Abstract: To analyze the roll calls in the US Senate in year 2003, we have employed the methods already used throughout the science community for analysis of genes, surveys and text. With information-theoretic measures we assess the association between pairs of senators based on the votes they cast. Furthermore, we can evaluate the influence of a voter by postulating a Shannon information channel between the outcome and a voter. The matrix of associations can be summarized using hierarchical clustering, multi-dimensional scaling and link analysis. With a discrete latent variable model we identify blocs of cohesive voters within the Senate, and contrast it with continuous ideal point methods. Under the bloc-voting model, the Senate can be interpreted as a weighted vote system, and we were able to estimate the empirical voting power of individual blocs through what-if analysis.
Abstract: Although group cohesion studies are rather common elsewhere, the last analyses of the Finnish parliament Eduskunta were published in the 1960s. This article provides, firstly, a fresh group cohesion analysis using the Agreement Index, which is a modified version of the classic Rice index. Secondly, two advanced voting similarity analyses, together with a new easy-to-understand way of illustrating the results, are provided. Where the Agreement Index operates at the parliamentary party group level, the voting similarity analyses are able to analyse and illustrate the individual MP level. The article is partly methodological in testing the voting similarity methods, however, it also provides insight into the recent voting behaviour within Eduskunta.
We are providing all the data and the source of our software so that our results can be reproduced. There is not much documentation, so only delve into this if you are a hacker.
Several other researchers in political science are working on voting data, and are kind enough to share their work on the Web:
Other software, kindly provided online: